ВЕТРОВАЯ НАГРУЗКА 10

Отдельные аспекты взаимодействия между реакцией сооружения и явлениями, происходящими в жидкости, представлены на рис. 6.6 16.15, 6.38], из которого следует, что возрастание амплитуды вынужденных гармонических колебаний кругового цилиндра приводит к увеличению коэффициента корреляции вихревого потока по его длине (на рис. 6.6 η = y_макс/D, y_макс -амплитуда колебаний, D — диаметр).

Амплитуды вызванных потоком колебаний цилиндрических сооружений в свою очередь зависят от массы и жесткости сооружения, а также от его демпфирующих свойств. На рис. 6.7 [6.39] показано влияние демпфирования на поперечные колебания круговой цилиндрической консольной вытяжной трубы высотой L, обтекаемой потоком, характеризуемым плавным течением со скоростью U. Из него видно, что среднее квадратическое значение приведенного перемещения η снижается более чем в 10 раз при увеличении относительного демпфирования с 0,002 до 0,009. Это снижение происходит не только из-за уменьшения величины передаточной функции системы, но также и вследствие снижения коэффициента корреляции по длине цилиндра (см. рис. 6.6). В этом случае происходит изменение амплитуды колебаний вытяжной трубы по высоте.

6.2. Галопирование поперек воздушного потока

Галопирование — аэродинамическая неустойчивость, характерная для гибких сооружений с особыми формами поперечного сечения, такими, как, например, прямоугольные или D-образные сечения, или эффективные сечения некоторых покрытых льдом проводов линий электропередачи. При определенных условиях, которые будут сформулированы в этой главе позже, в таких сооружениях возможны колебания с большими амплитудами в перпендикулярном потоку направлении (в 10 или даже в значительно большее число раз превышающими размеры самого сечения в этом направлении) при частотах, которые значительно ниже частот срыва вихрей, характерных для того же самого сечения. Классическим примером такого типа аэродинамической неустойчивости является галопирование с большими амплитудами поперек воздушного потока проводов линий электропередачи, которые покрылись слоем льда под дождем с образованием гололеда.

Результаты изучения проблемы галопирования опубликованы в работах [6.40—6.42]. В работах [6.43—6.50] галопирование рассматривается как нелинейное явление. При галопировании поперек воздушного потока относительный угол атаки ветром поперечного сечения сооружения находится в прямой зависимости от скорости сооружения

в перпендикулярном потоку направлении. Имеющийся опыт показывает, что знание средних коэффициентов подъемной силы и сопротивления поперечного сечения, полученных в статических условиях на неподвижном объекте в виде функций угла атаки, служит достаточной основой для построения удовлетворительного аналитического описания явления галопирования. Таким образом, галопирование управляется по существу квазистационарными силами. Подобно случаю вихревого возбуждения колебаний, оно будет рассматриваться и описываться аналитически как двумерное по своей природе явление. Другие вопросы, связанные с реакцией при галопировании, рассмотрены в работах [6.46—6.50].

6.2.1. Аналитическая формулировка проблемы галопирования. Прежде чем привести основную аналитическую формулировку явления, представляет интерес отметить некоторые из общепризнанных работ, в которых рассматривается галопирование. В [6.48] дается обзор состояния вопроса, проведен сжатый анализ проблемы, а также отмечены ранние и основные исследования Глауэрта [6.40] и Ден- Гартога [6.41, 6.42]. Работы [6.43—6.49] являются важным вкладом подробного описания механизма галопирования необходимо иметь полное разложение C_Fv в ряд по степеням y/U. В [6.48] предлагается укороченный степенной ряд, состоящий из нескольких членов с нечетными степенями y/U и одного члена второй степени, взятого с соответствующим знаком, для сглаживания экспериментальных данных:

Если зависимость Cl и C_D от α известна, то коэффициенты с А₁ по А₇, включительно можно оценить следующим образом. Сначала строится график зависимости C_fy от tg а. Поскольку tgα = y/U, то C_fy можно аппроксимировать многочленом (6.46), используя метод наименьших квадратов или какой-либо другой. В [6.48] для решения получаемого нелинейного уравнения применен метод Крылова—Боголюбова; при этом в качестве первого приближения для реакции постулируется

где а и φ — рассматриваются как медленно изменяющиеся функции времени.

Отдельные интересные особенности решения выходят за рамки данного раздела. Тем не менее достаточно указать на тот факт, что характерные нелинейные явления при галопировании, встречающиеся в эксперименте, хорошо прогнозируются на основе теоретических результатов, получаемых для квазистационарной модели. Например, могут быть непосредственно предсказаны известные нелинейные явления «скачка» амплитуды (когда они имеют место).

- В [6.49] продолжены исследования [6.48] по изучению реакции при галопировании, а также выявлены три основных типа зависимости C_fy от α и соответствующая им амплитуда реакции при галопирования α как функция приведенной скорости U/Dω₁ (см. рис. 6.11). Отмечено, что единственно возможные колебательные движения — это движения с амплитудами а, которые показаны сплошными линиями на рис. 6.11. В [6.49] также исследованы реакции протяженных трехмерных тел с помощью рассмотренной выше теории для двумерного потока и описано влияние турбулентности потока на галопирование. Отмечено, что одни и те же факторы могут оказывать различное влияние на осредненные значения C_L и С_D в зависимости от масштабов и вида спектра турбулентности потока. Например, в зависимости от конкретных обстоятельств турбулентность может способствовать или препятствовать созданию необходимых условий для возникновения галопирования. Наконец, в [6.49] выявлено, что если начальное возмущение больше амплитуды установившихся колебаний, то могут быть случаи галопирования, для которых критерий Ден-Рартога не удовлетворяется.

В [6.54] анализируется весьма близкая задача для длинной гибкой балки, имеющей возможность изгибаться как вдоль, так и поперек воздушного потока. Работа [6.55] посвящена изучению воздействия ветра, направленного под косым углом к продольной оси галопирующего тела.

6.3. Галопирование в спутной струе

Рассмотрим случай обтекания двух цилиндров, один из которых расположен выше по течению относительно другого. В определенных условиях цилиндр, расположенный ниже по течению, может испытывать колебания типа галопирования, вызванные турбулентной спутной струей от первого цилиндра. Именно такой случай имеет место, например, для проводов расщепленной фазы линий электропередачи, сгруппированных в так называемые пучки, т. е. группы проводов, состоящие из двух, четырех, шести, восьми или более параллельных проводов, отделенных друг от друга с помощью распорок в поперечном к их пролету направлении. На рис. 6.12 показана распорка между четырьмя параллельными проводами расщепленной фазы линии электропередачи. При установленных распорках именно участок провода между ними наиболее восприимчив к галопированию в спутной струе, так как здесь провод имеет наибольшую свободу перемещений.

Галопирование в спутной струе может происходить только в условиях, когда частоты колебаний цилиндра, расположенного ниже по течению, меньше частот образования за ним вихрей, и соответствующих частот для цилиндра, расположенного выше по течению. Точно так же, как и для явления, рассмотренного в подразд. 6.2, галопирование в спутной струе определяется параметрами, которые описывают аэродинамические процессы в среднем (а не их текущие значения), и могут быть измерены, когда тело является неподвижным.

Спутная струя цилиндра, расположенного выше по течению, может быть изображена, как показано на рис. 6.13. При исследовании этой спутной струи «зондом», который сам фактически является цилиндром, расположенным ниже по течению, выявляется характер распределения сил, действующих на этот цилиндр в направлении ветра и в поперечном направлении (рис. 6.14), при расположении зонда в отдельных точках спутной струи. Принципиально важный результат, полученный в экспериментальных исследованиях, состоит в том, что силы, действующие в спутной струе поперек потока, стремятся переместить цилиндр, расположенный ниже по течению, к оси (средней линии) спутной струи. Это происходит вопреки, казалось бы, интуитивному ожиданию обратного, что, поскольку внешний поток за пределами спутной струи имеет большую скорость, он должен был бы, согласно уравнению Бернулли, стремиться вытолкнуть расположенный ниже по течению цилиндр во внешние слои, от центра спутной струи.

Этой кажущейся аномалии пытались найти объяснение. Ориентировочно ее можно отнести за счет многочисленных перекрещиваний поля скоростей потока в пределах спутной струи, вызванных изменяющимися во времени местными струйными течениями жидкости, которые имеют мощные составляющие, направленные внутрь, к центру. Эти струйные течения, или местные скорости жидкости стремятся вызвать периодически повторяющиеся силы лобового сопротивления, направленные в среднем к оси спутной струи. Указанное объяснение явления было в какой-то мере подтверждено исследованиями потока методом визуализации в гидродинамической трубе [6.56]. 

Как показано на рис. 6.14, центрирующая подъемная сила (действующая на цилиндр в направлении к оси спутной струи) достигает наибольшего значения примерно в четверти ширины спутной струи.

Когда цилиндр, расположенный ниже по течению от другого тела и отстоящий на несколько диаметров позади него, смещается (по любой причине) примерно во внешнюю четверть спутной струи (см. рис. 6.13), то он попадает в зону неустойчивости при галопировании. В этой зоне начнется галопирующее движение с возрастанием амплитуды, которое будет происходить до тех пор, пока не достигнет своего предельного цикла. Это движение представляет собой колебания большой амплитуды, происходящие по эллиптической траектории с длинной осью эллипса, ориентированной примерно вдоль направления основного потока. Направление эллиптической траектории таково, что цилиндр движется вниз по потоку около внешней границы спутной струи и против потока ближе к ее оси или по часовой стрелке над осевой линией (см. рис. 6.14) и против часовой стрелки под нею. Эти направления движения совпадают с интуитивной оценкой того, что результирующие силы сопротивления будут больше в наружной, более быстрой части спутной струи и меньше во внутренней. Работы [6.56—6.65] охватывают различные аспекты явления галопирования в спутной струе. На рис. 6.15 [6.63] показана запись развития траектории галопирования в спутной струе, полученная с помощью осциллоскопа.

6.3.1. Анализ явления галопирования в спутной струе. Это явление анализируется с позиций двумерной задачи, как это уже делалось в предшествующих разделах. Рассмотрим два цилиндра (рис. 6.16): один из них является наветренным (расположен выше по течению и создает спутную струю), а другой — подветренным (находится в пределах этой струи). Предположим, что подветренный цилиндр упруго оперт в горизонтальном и вертикальном направлениях и занимает некоторое положение (X, Y), где X,Y — координаты в направлении ветра и в поперечном направлении, которые удобно отнести к наветренному цилиндру.

Уравнения движения для подветренного цилиндра могут быть составлены путем записи отклонений х,у этого цилиндра от положения, определяемого координатами X,Y:

Далее, если С_х и С_у определены как коэффициенты, соответствующие среднему значению силы при установившихся колебаниях и отнесены к динамическому давлению (скоростному напору) невозмущенного потока ¹/₂ ρU², которое приложено к цилиндру, находящемуся в точке с координатами (X, Y), то можно показать, что в начальной стадии движения силы в направлении х и у выразятся в виде [6.65].

Выражения, подобные (6.49), были впервые выведены в [6.58 и 6.59]. Значения С_х,С_у и их производных получаются путем непосредственного измерения осредненных по времени значений при испытании модели в аэродинамической трубе. Представляют интерес случаи гладких круговых цилиндров и имеющих более шероховатую поверхность витых многожильных проводов (см. также гл. 8).

Аналитическое решение задачи, при котором силы, определяемые выражениями (6.49), явно представляют собой аэродинамические силы при самовозбуждающихся колебаниях, ищется в предположении, что перемещения в (6.48) и (6.49) имеют значения приравнивая нулю определитель, составленный из коэффициентов уравнений (6.48).

Из (6.50) следует, что полученные решения соответствуют аэроупругой неустойчивости, если в выражении λ = λ₁+iλ₂ (где i = √-1)λ₁ ≥ 0, так как в этом случае они содержат расходящийся экспоненциальный сомножитель. Затем такие решения находят для параметров, соответствующих ряду точек при других значениях координат X,Y.

Между теорией и экспериментом, как это следует из рис. 6.17 [6.56], наблюдается удовлетворительная согласованность. Кривые на рисунке связывают точки, в которых найдены решения, характеризующие границы области неустойчивости (т. е. где λ = iλ₂). По этим решениям, если есть необходимость, можно вычислить траекторию движения цилиндра [х (t), у (t)] с помощью уравнений (6.48) и (6.49).

Как и при других явлениях аэроупругих колебаний, параметры сооружения оказывают сильное влияние на характеристики галопирования в спутной струе. В частности, при проведении исследований на моделях необходимо уделить особое внимание значениям коэффициентов жесткости K_rs (r,s = х, у). Прежде всего, это относится к воспроизведению работы проводов — вопрос, который очень подробно рассмотрен в работах [6.60, 6.62, 6.65], и выходит за рамки настоящего исследования.

6.4. Дивергенция

Явление дивергенции первоначально связывалось, прежде всего, с крыльями самолета и их подверженностью скрутке при некоторой предельной скорости воздуха. Чтобы мысленно представить, что происходит в этом случае, рассмотрим аэродинамическую поверхность малой относительной толщины или любую другую аналогичную конструкцию (такую, например, как пролетное строение висячего моста) (рис. 6.18). Под действием ветра конструкция будет нагружена (и в свою очередь оказывать им противодействие) силой лобового сопротивления, подъемной силой и аэродинамическим крутящим моментом. С увеличением скорости ветра последний из этих силовых факторов будет также увеличиваться.

Это приведет к дальнейшему закручиванию конструкции. Однако такое ее состояние, за счет увеличения эффективного угла атаки ветра, может способствовать еще большему увеличению аэродинамического крутящего момента, для уравновешивания которого потребуется дополнительный реактивный момент в конструкции. Наконец, достигается такая скорость, при которой вызванный ветром момент вместе с продолжающейся тенденцией к закручиванию конструкции, требующей с ее стороны дополнительного увеличения реакции, создает неустойчивое состояние и конструкция разрушается.

Рассматриваемая проблема — это проблема устойчивости и в этом смысле совершенно аналогична проблеме потери устойчивости колонны при продольном изгибе. Точно так же, как потеря устойчивости колонны при продольном изгибе происходит при действии на нее критической нагрузки, дивергенция возникает при некоторой критической скорости дивергенции ветра. Это явление зависит от гибкости сооружения и от того, в какой степени скручивание конструкции вызывает нарастание действующих на нее аэродинамических моментов. Оно не зависит от предела прочности конструкции.

В случае аэродинамической поверхности малой относительной толщины аэродинамический крутящий момент увеличивается с увеличением угла атаки. Возможно, что для более сложных сооружений аэродинамический крутящий момент не следует этой простой зависимости, в результате они могут вести себя не так, как описано выше. В ряде случаев в зависимости от соотношения между аэродинамическим моментом и углом атаки некоторые сооружения могут быть устойчивыми к дивергенции. И, наконец, следует отметить, что в большинстве случаев, представляющих практический интерес для гражданского строительства, критические скорости дивергенции исключительно высоки и выходят далеко за пределы скоростей, обычно рассматриваемых при проектировании сооружений.

6.4.1. Аналитическое моделирование дивергенции. Для анализа явления дивергенции рассмотрим (см. рис. 6.18) поперечное сечение конструкции, повороту которого относительно некоторого центра вращения (или центра жесткости), противодействует торсионная пружина. Обозначим коэффициент жесткости пружины и угол поворота соответственно через k_a и а. Примем, что средняя скорость ветра U, а ширина настила моста В, тогда аэродинамический момент, приходящийся на единицу длины пролета, можно записать в виде

Пример зависимости С_М от а для поперечного сечения моста, имеющего балку жесткости со сквозными фермами, показан на рис. 6.19. При нулевом угле атаки значение этого момента равно:

При небольшом отклонении α от значения α = 0 М_а может быть задан в первом приближении в виде

Приравнивая аэродинамический момент внутреннему моменту конструкции, получаем

В результате задача о дивергенции (в такой двумерной постановке) сводится к уравнению (6.54). Рассмотрим теперь его решение.

ОбозначимВ таком случае уравнение (6.54) прини мает вид

или

Решение уравнения (6.56) при α, стремящемся к бесконечности (наступление дивергенции), будет удовлетворяться для значения

Следовательно, последнее определяет критическую скорость дивергенции

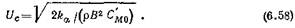
Эту задачу можно легко обобщить для пространственного случая, это будет сделано на примере отдельного частного случая (см. гл. 8). Следует также отметить, что в этой задаче рассматривается только начальная стадия неустойчивости. Если же с увеличением скорости поведение конструкции становится более сложным (например, вследствие более сложной зависимости С_М от α, чем это показано на рис. 6.19), то задача о дивергенции может быть решена путем последовательного удовлетворения соотношения

для любого интересующего диапазона скоростей.

6.5. Флаттер

Флаттер аэродинамических поверхностей — один из наиболее рано распознанных видов аэроупругих колебаний. Термин «флаттер» имел различные смысловые значения. Однако в настоящее время этот термин употребляют с использованием дополнительных определений, например классический флаттер, срывной флаттер, флаттер системы с одной степенью свободы, панельный флаттер. Все эти термины первоначально использовались в авиационно-космических исследованиях, но некоторые из них были перенесены в инженерные исследования ветровых воздействий.

Термин классический флаттер сначала использовали применительно к аэродинамическим поверхностям малой относительной толщины. Сейчас его также применяют при изучении колебаний висячих мостов. Под этим термином подразумевается явление аэроупругости, при

котором динамические перемещений, соответствующие двум степеням свободы сооружения (повороту относительно продольной оси и вертикальному смещению), становятся связанными при неустойчивых колебаниях, возбуждаемых воздушным потоком. Взаимосвязь колебаний, соответствующих двум степеням свободы (необходимое условие для флаттера аэродинамической поверхности малой относительной толщины), стала отличительной чертой классического флаттера.

Срывной флаттер — это крутильные колебания аэродинамической поверхности как системы с одной степенью свободы, возбуждаемые за счет нелинейных характеристик подъемной силы в окрестностях наступления срыва потока или в условиях потери подъемной силы. Это явление также наблюдается в конструкциях, имеющих широкие поверхности, при обтекании которых происходит срыв потока в зависимости от угла атаки набегающего потока. Так называемый флаттер знаков «стоп» (крутильные колебания знаков дорожного движения типа «стоп» относительно стоек крепления, обладающих малой жесткостью на кручение) служит примером, взятым не из области аэронавтики.

Флаттер системы с одной степенью свободы может включать в себя срывной флаттер, но может быть просто связан с системами, подверженными действию интенсивных срывных течений. Типичными примерами тому являются плохообтекаемые, расположенные поперек линий тока тела. Важное вместо среди них занимают пролетные строения висячих мостов, которые могут в ряде случаев при крутильных колебаниях проявлять неустойчивость как системы с одной степенью свободы. Более подробно эти случаи рассмотрены в гл. 8.

Панельный флаттер — это незатухающие колебания панелей (типичные для поверхностей корпусов больших ракет), вызываемые распространением вдоль них с высокой скоростью потока воздуха. Наиболее наглядно они проявляются при сверхзвуковых режимах течения и поэтому не наблюдаются в ситуациях, встречающихся при инженерных исследованиях ветровых воздействий. Тем не менее флаттер туго натянутых брезентовых покрытий и флаттер флагов связаны с панельным флаттером.

При детальном изучении флаттера почти во всех случаях обнаруживаются нелинейные аэродинамические эффекты. Однако в ряде ситуаций оказалось возможным успешно решить задачу на основе линейных аналитических подходов. В пользу этого свидетельствуют два основных довода. Во-первых, несущая конструкция обычно рассматривается как линейная упругая система, и при ее работе доминирующей является такая форма реакции, которой обычно соответствуют гармонические колебания с амплитудой, изменяющейся по экспоненте. Во-вторых, именно в начальной стадии процесса (при его зарождении), которую можно рассматривать как характеризующуюся лишь небольшими амплитудами колебаний, происходит разделение устойчивого и неустойчивого режимов. Эти две основные особенности дают возможность проводить анализ флаттера на основе обычного рассмотрения устойчивости линейных упругих систем.

Характерным для флаттера как типичного процесса автоколебаний является то, что система за счет своих перемещений (и их производных по времени) перекачивает энергию из воздушного потока. Если системе задано начальное возмущение, то ее дальнейшие перемещения будут затухать или нарастать (т. е. амплитуды ее колебаний будут уменьшаться или неограниченно увеличиваться) в зависимости от того, будет ли энергия движения, получаемая от потока, меньше или больше энергии диссипации системы вследствие конструкционного демпфирования. Тогда теоретическая линия раздела между случаями затухания и нарастания амплитуды, т. е. характеризующая установившиеся гармонические колебания, принимается соответствующей критическому условию возникновения флаттера.

При рассмотрении явления флаттера применительно к современным инженерным исследованиям ветровых воздействий ограничимся только классическим флаттером и флаттером системы с одной степенью свободы.

6.5.1. Уравнения движения для поперечного сечения аэродинамической поверхности или балки жесткости моста. Рассмотрим поперечное сечение аэродинамической поверхности или балки жесткости моста (рис. 6.20), находящегося под действием набегающего потока с плавным течением. Принимаем, что сечение имеет две степени свободы, соответствующие перемещениям при изгибе и кручении, которые обозначаем соответственно через h и α. Механическая система на единицу длины характеризуется массой т, моментом инерции l, статическим моментом масс S (равным произведению массы т на расстояние α между центром масс и центром жесткости), вертикальной восстанавливающей силой и восстанавливающим крутящим моментом, задаваемыми с помощью коэффициентов упругости C_h и С_а, и коэффициентами сопротивления c_h и с_а. Используя эти определения, уравнения движения можно записать в виде [6.66, 6.67]:

При симметричных поперечных сечениях мостов центр масс расположен в вертикальной плоскости, проходящей через геометрическую ось сечения. В этом случае α = 0. Как правило, ось вращения также лежит в этой плоскости, хотя она может отстоять на некотором расстоянии по вертикали от центра масс. Для мостов с арочным профилем проезжей части ось вращения может лежать значительно ниже этого центра. При анализе динамики поперечного сечения моста момент инерции I определяется относительно оси вращения и, следовательно, является обычно (даже при постоянном поперечном сечении) величиной, изменяющейся по длине пролета.

Определение фактического положения оси вращения относится к задачам, выходящим за рамки настоящей книги.

Э.Симиу, Р.Сканлан
Воздействие ветра на здания и сооружения
1984